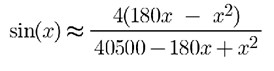Go here to sign up for The Embedded Muse.
The Embedded Muse Logo The Embedded Muse
 Issue Number 456, October 17, 2022
Copyright 2022 The Ganssle Group

Editor: Jack Ganssle, jack@ganssle.com
   Jack Ganssle, Editor of The Embedded Muse

You may redistribute this newsletter for non-commercial purposes. For commercial use contact jack@ganssle.com. To subscribe or unsubscribe go here or drop Jack an email.

Contents
Editor's Notes

SEGGER Embedded Studio cross platform IDE

Tip for sending me email: My email filters are super aggressive and I no longer look at the spam mailbox. If you include the phrase "embedded muse" in the subject line your email will wend its weighty way to me.

There's an interesting article about Ted Hoff, inventor of the 4004, here.
Quotes and Thoughts

Scientists dream about doing great things. Engineers do them. James A. Michener

Tools and Tips

Please submit clever ideas or thoughts about tools, techniques and resources you love or hate. Here are the tool reviews submitted in the past.

Steve King had an interesting point about sending debug data to the cloud:

Just a word of caution when using tools like DevAlert to send diagnostic data to "the cloud".  Make sure that's an opt-in feature!  Yeah, it's just debugging data to us developers, and usually we don't care what the content is except as it pertains to the errors.  But, depending on the device, it might actually reveal sensitive data that the user doesn't want to disclose. To make a simple concrete example, think of a networked garage door opener. Diagnostic data might include its location, or its keypad PIN, wifi password, etc. Leaked data might give someone access to the building.

Even if you anonymize all the data and wrap it in the most secure encryption ever, just the fact that a diag pack is being transmitted could be enough to compromise the user.  It lets an attacker know what manufacturer's equipment is being used, which might allow them to use an attack unrelated to the data itself.  Diag data is being sent back to XYZ Corp; XYZ Corp's keypad has a hardware flaw that opens the door if you short the power supply while holding the 6 and 3 keys. All an attacker has to do is scan neighborhood wifi connections to see which houses are contacting XYZ Corp periodically and they're in.  I admit it's far-fetched, but most security scenarios are. Right up until they suddenly aren't.

I don't mean to pick on DevAlert. I know nothing of that product and what I'm saying isn't specific to it.  It applies to any way you transmit diag data. Log the data onboard, sure, but give the user control over when it gets sent.  Once you've sold the device it's no longer yours, and neither is the data.

Jakob Engblom had a contrary opinion about subscription-based tools:

I read the comments on subscription-based tools and software in the Embedded Muse #453 and #454 and  #455.  It is pretty horrific when subscriptions are just used for price-gouging on things that would seem to be stable, I must argue that there are cases where it makes sense.  I wrote a blog about it five years ago, see
https://jakob.engbloms.se/archives/2552

In short: having worked with selling and developing software for professional usage, I am actually much happier with a subscription model where all customers get all updates all the time (if they want them).

The alternative is forcing "new features" into the product whether needed or not to entice users to upgrade, and it can mean delaying new features to make a new version more attractive, when it would be better for all users to have the new feature now.

Having a model where we can simply continuously add and update functionality (and sometimes remove stuff that is getting old) without having to artificially tie it to "major versions" of the product is really good. It makes it more fun to develop the product itself, and fits better with what people have come to expect from the open-source world and web-world of constant change.

Here's a nice intro to the Rust programming language.
Freebies and Discounts

Kaiwan Billimoria kindly sent us three copies of his new book Linux Kernel Debugging for this month's contest. It's a massive tome, at 600+ pages that anyone working on Linux internals would profit from.

Enter via this link.
Math Approximations

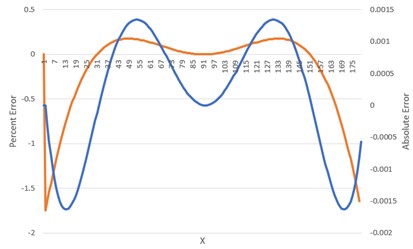
I'm fascinated by approximations. In the embedded world we often aren't running a monster machine that has built-in trig or even floating point. I've written quite a bit about floating point approximations to trig and other functions, but what happens when you need a fast sine or something similar, with limited precision? It's often possible to stick with integer math to get a pretty decent approximation. Though a lookup table is the fastest approach, those tend to eat a lot of memory.

I recently stumbled across a couple of fun approximations you might find useful.

First, did you know that 355/113 is very close to pi? It's 3.1415929, not far from the nearly-true value of 3.1415926.

How about e, the base of the natural logs? Try 271801/99990, which is 2.718281828. Or, there's 3020/1111 which is 2.71827.

Trig functions are a little more complicated, but here's a cool approximation for the sine, using degrees as the input argument:

(Obviously, this would have to be normalized to your range of integers).

This is valid over the range of 0 to 180 degrees.

Errors from actual values are small. This graph shows the absolute errors in blue and percentage error in orange:

You can calculate 180x and x2 once, then use them twice.

Cosine is just sine shifted by 90 degrees. Be warned: as mentioned, the sine approximation is accurate only to 180 degrees; after that errors are large. If you compute cos=sin(x+90) be sure x never exceeds 90, as the result won't make sense. Reduce x to 0 to 90 degrees (i.e., the first quadrant) using ideas from here.

If you're working in radians and can constrain the input argument to 0 to 0.35 radians (0 to 20 degrees) then an even faster algorithm is: sin(x)=x. That's accurate to about 2% over that range.
Fast Clocks Might Not Be Fast

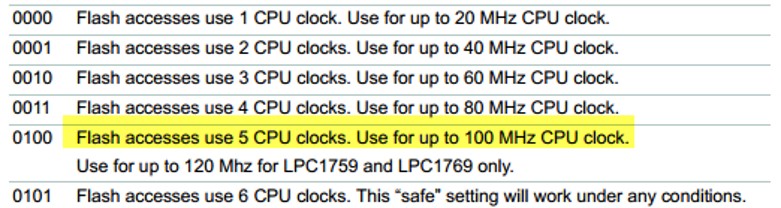
Using a fast algorithm like the one above above is one way to gain performance. Another is to beef up the hardware. But that's not always as simple as one might hope. Often doubling the clock rate of a CPU won't gain a lot of improvement. Memory is a bottleneck. Consider this warning from one MCU datasheet:

A processor that executes instructions in a single cycle may require many wait states at higher clock rates. While certain aspects of performance might improve you may be very disappointed with the results.

Of course, one could copy the code to fast RAM and run from there, but that comes at the cost of the additional memory.

As always, read the datasheets very carefully!
Source Controlling Tools

Steve Foschino poses a question that's worth pondering.

I'm wondering how others in the embedded world are dealing with source controlling commercial development tools.  When  development tools came on disk, it was easy to put the disk in a safe place and it was readily available to be installed on a new machine.  Later, as repositories came into play, we could store copies of the install media in the repository for future use.  Updates (rarely applied) were typically files that needed to be run on the installed tool.  Then, as internet access became more available, you were able to download the programs, run the installer, and put the installer in the repository.  Today, however, vendors are supplying their own IDEs that are downloaded via a link from their website.  This link may not even the installer but just a link to the downloader running on their website, so there’s nothing to place under source control; the tool just installs itself.  There’s no promise of how long a version of the tool will be available. When needed later on, the link to the website could be bad.  At my job, in addition to our newer stuff,  we support a code base that can be 30 - 35 years old.  For this older codebase, we can go to the safe or the repository, get the tools used to create it, spin up a VM of the correct OS flavor, rebuild the source, compare the compiled file to the project repository and be 100% certain we are starting with the correct code and start the maintenance from there.  How do you do this with today’s tools, 15 years later with a subscription based IDE that was downloaded from a vendor website that no longer exists?.  YIKES!

Even though new tool versions become available, in our embedded world, newer isn't always better.  We aren't always in a position to sacrifice years of code maturity just because a new, shiny UI is available or support for newer devices have been included in the IDE.  Unlike the PC/online world, we aren't re-writing stuff from the ground up every year in the language of the day.  We can’t just tell a customer to "update to the latest version" to get a bug fix.  We use C in our products.  With today’s IDEs with in-program auto updates, libraries all over the place and compilers/linkers for multiple device support and no formal installer, it’s impossible to capture these tools for the future.  And subscription based software make this even worse.   I'm sure we are all facing this configuration problem to some degree and I'm wondering how others in the embedded world are dealing with it.

Any thoughts? I just put a new computer together and wound up downloading the newest versions of the tools I use. But what happens if a tool vendor goes extinct? Or discontinues the products? Or you need an Internet connection to a now-defunct company to register the product before it works?

We have seen this in the past in the embedded space. Back before the dot.com meltdown there was a frenzy of acquisitions; Wind River bought a number of tool vendors, and most of those products are now long gone. (A friend who worked for one of these vendors told me he worked for 5 companies over two months without changing jobs as the businesses were acquired.)

(And, to carry on the subject of speedups from the articles above, I found stunning improvements in the speed of most Windows software by using big NVMe SSDs. However, it's important to spend a few extra bucks to get PCI versions rather than the SATA parts. Disk-intensive applications benefit from using two such SSDs; one for C: and the other for D:, as the code can ping pong accesses between them. A processor with lots of cores, these SSDs, and plenty of RAM shortened one task from 4 days of compute time to two hours.)
Failure of the Week

Have you submitted a Failure of the Week? I'm getting a ton of these and yours was added to the queue.

From Jerry Penner:

 

Another NaN from David Rea:
Jobs!

Let me know if you’re hiring embedded engineers. No recruiters please, and I reserve the right to edit ads to fit the format and intent of this newsletter. Please keep it to 100 words. There is no charge for a job ad.
Joke For The Week

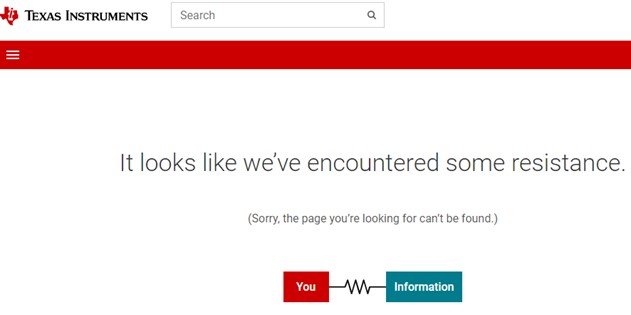
These jokes are archived here.

Harold Kraus found TI has a fun 404 message:
About The Embedded Muse

The Embedded Muse is Jack Ganssle's newsletter. Send complaints, comments, and contributions to me at jack@ganssle.com.

The Embedded Muse is supported by The Ganssle Group, whose mission is to help embedded folks get better products to market faster.